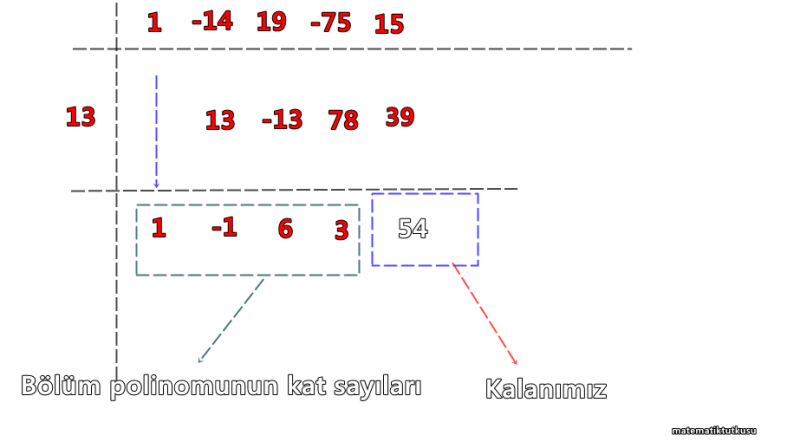
Soru 1
P(x) = x⁴-14x³+19x²-75x+15 polinomunun x-13 ile bölümünden kalan kaçtır ?
Çözüm
Görüldüğü gibi kalanı 54 olarak bulduk.
Yukarıdaki çözüm horner metoduyla çözülmüştür.İstersek x yerine 13 yazarakta kalanı bulabiliriz.
-----------------------------------------------------------------------------------
Soru 2
P(x) = x⁴+2x³+ax+b polinomunun (x-1)² ile kalansız bölünebilmesi için b kaç olmalıdır ?
Çözüm
P(x)=(x-1)².Q(x)+K
P(x)=0 olması için
P(1)=0 olması gerekir.
Aynı zamanda ifadenin kendisi ve birinci türevi de 0 olmalıdır. İlk önce ifadenin birinci türevini bulalım.
P'(1)=4x³+6x²+a = 0
P'(1)=4+6+a=0
P'(1)=a=-10
P(x)=x⁴+2x³+ax+b=0 olacaktır.
P(1)=1+2+a+b=0
P(1)=a+b=-3
a=-10
b=7 bulunur.
Türev nasıl alınır ? Bilmiyorsanız , Trev konu anlatm video zml sorular testi z izle indir
-----------------------------------------------------------------------------------
Soru 3
P(x) polinomu x²+4 ile bölündüğünde kalan 2x+1 olduğuna göre P²(x) polinomu x²+4 ile bölündüğünde kalan aşağıdakilerden hangisi olur ?
Çözüm
P(x)=(x²+4).Q(x)+(2x+1)
P²(x)=((x²+4).Q(x)+(2x+1))²
x²=-4 yazarsak
P²(x)=((0).Q(x)+(2x+1))²
P²(x)=4x²+4x+1
x²=-4
-16+4x+1
4x-15 bulunur.
-----------------------------------------------------------------------------------
Soru 4
(x-2).P(x)=x³-2x+m olduğuna göre P(x) polinomunun x-2 ile bölümünden kalan kaçtır?
Çözüm
İlk önce m'yi bulalım x=2 diyelim
0=8-4+m
0=4+m
m=-4 bulunur.
(x-2).P(x)=x³-2x-4
P(x)=x²+2x+2 olur
P(2)=4+4+2
P(2)=10 bulunur.
-----------------------------------------------------------------------------------
Son sorumuzu da kolay bir şeyle noktalayalım
Soru 5
P(x)=x²-4x+m
olmak üzere P(x-2)'nin sabit terimi -6 olduğuna göre , m kaçtır ?
Çözüm
P(x-2)'nin sabit terimini bulmak için x yerine 0 yazarsak P(-2)'yi bulmamız gerekecektir.
P(-2)=-6 verilmiş zaten
P(x)=x²-4x+m ifade'de x yerine -2 yazalım.
P(-2)=4+8+m = -6
P(-2)=m+12=-6
m=-18 olur.